Complex networks modeling using fractional dynamics in the presense of hidden nodes/unknown unknowns
 |
The theme of this project lies in answering a big and interesting question of incorporating unknown artifact contribution towards Non-Markovian dynamics. Numerous real world systems, for example, brain, physiological signals, social networks, gene-regulatory networks etc. can be modeled accurately with fractional dynamics by including long-range memory and spatial correlations. However, the assumption of complete knowledge of the network may not hold in most of the experimental situations due to limited probing resources. The inclusion of unknown unknowns aims to answer this limitation by probabilistically adding the hidden effects in the observed data. The ongoing work is detailed in the following publications.
Dealing with unknown unknowns: Compact accurate modeling of brain EEG signals using fractional dynamics
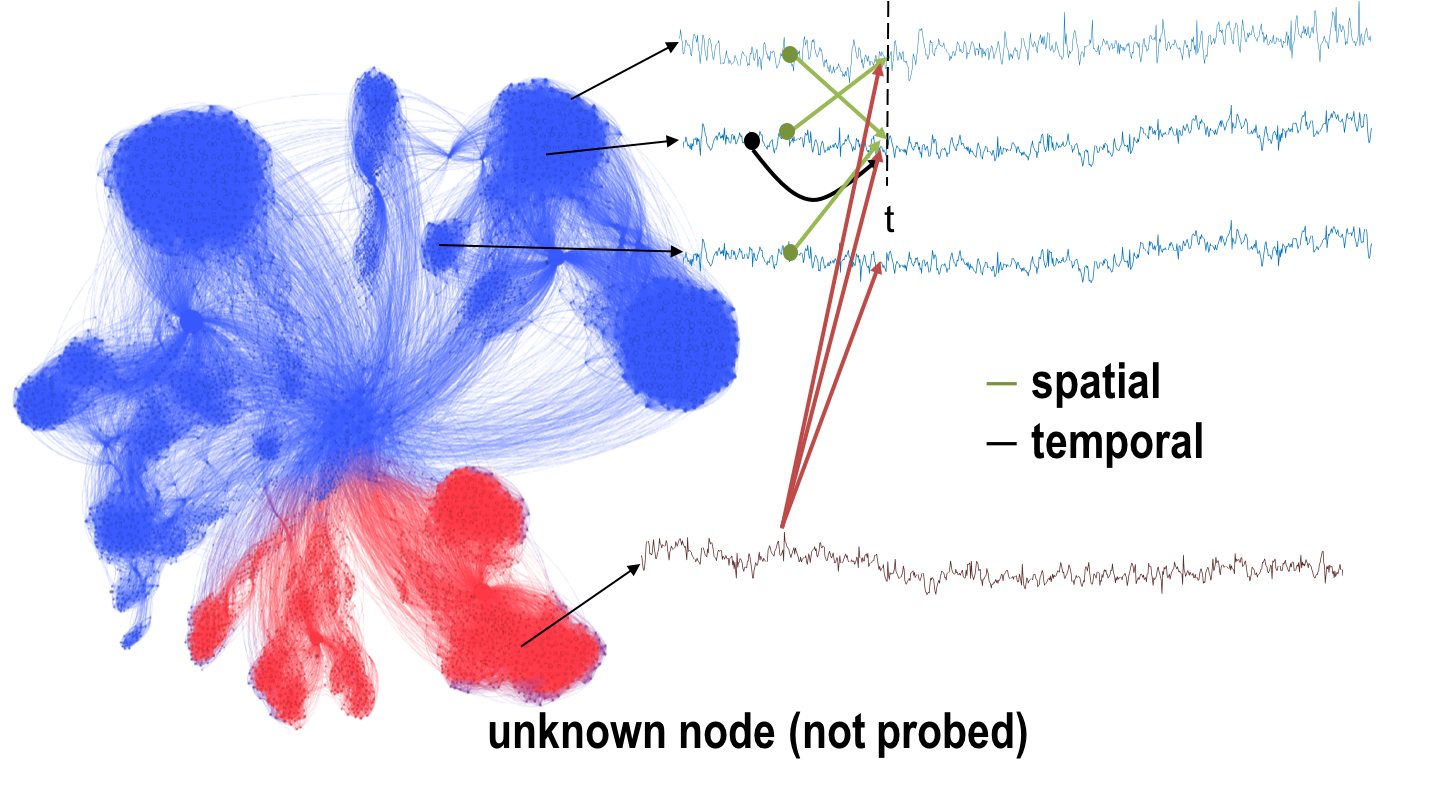
Abstract: This paper focuses on analysis and design of timevarying complex networks having fractional order dynamics. These systems are key in modeling the complex dynamical processes arising in several natural and man made systems. Notably, examples include neurophysiological signals such as electroencephalogram (EEG) that captures the variation in potential fields, and blood oxygenation level dependent (BOLD) signal, which serves as a proxy for neuronal activity. Notwithstanding, the complex networks originated by locally measuring EEG and BOLD are often treated as isolated networks and do not capture the dependency from external stimuli, e.g., originated in subcortical structures such as the thalamus and the brain stem. Therefore, we propose a paradigm-shift towards the analysis of such complex networks under unknown unknowns (i.e., excitations). Consequently, the main contributions of the present paper are threefold: (i) we present an alternating scheme that enables to determine the best estimate of the model parameters and unknown stimuli; (ii) we provide necessary and sufficient conditions to ensure that it is possible to retrieve the state and unknown stimuli; and (iii) upon these conditions we determine a small subset of variables that need to be measured to ensure that both state and input can be recovered, while establishing sub-optimality guarantees with respect to the smallest possible subset. Finally, we present several pedagogical examples of the main results using real data collected from an EEG wearable device.
[paper] [code]
Learning latent Fractional dynamics with Unknown Unknowns
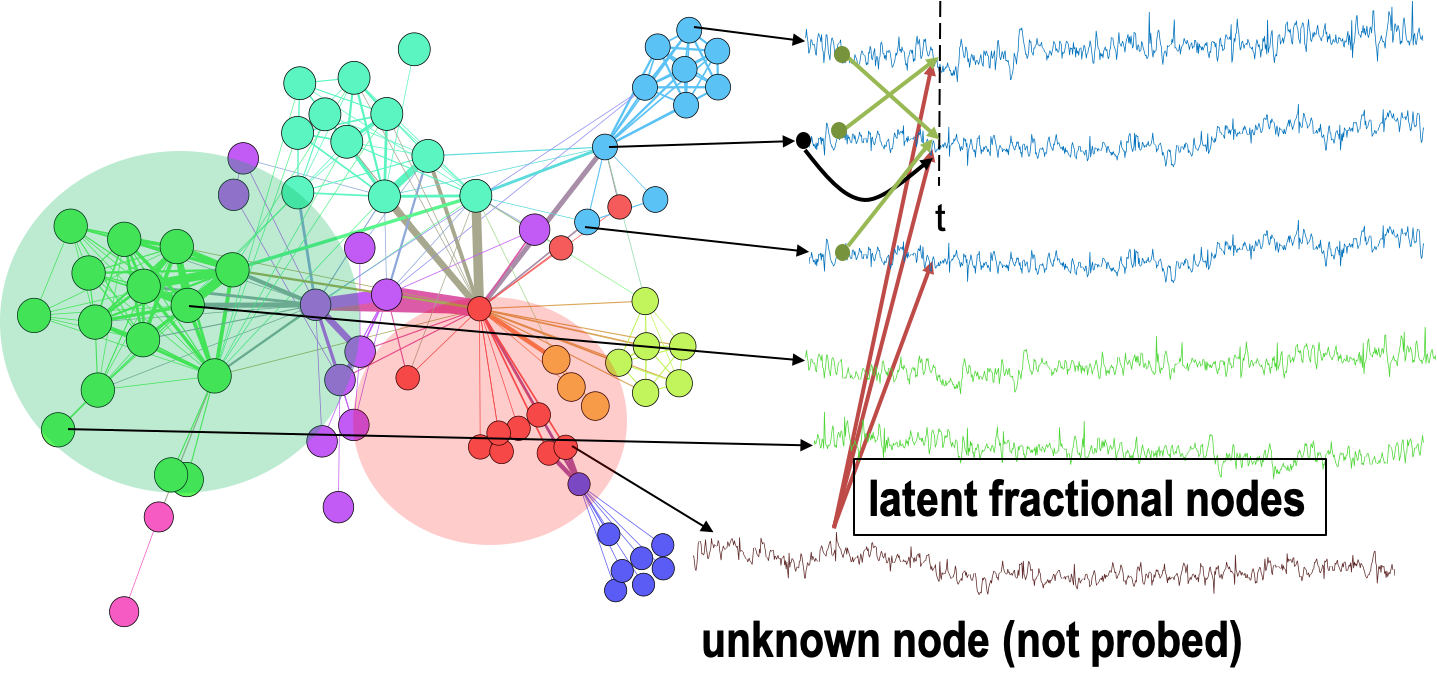 |
Abstract: Despite significant effort in understanding complex systems (CS), we lack a theory for modeling, inference, analysis and efficient control of time-varying complex networks (TVCNs) in uncertain environments. From brain activity dynamics to microbiome, and even chromatin interactions within the genome architecture, many such TVCNs exhibits a pronounced spatio-temporal fractality. Moreover, for many TVCNs only limited information (e.g., few variables) is accessible for modeling, which hampers the capabilities of analytical tools to uncover the true degrees of freedom and infer the CS model, the hidden states and their parameters. Another fundamental limitation is that of understanding and unveiling of unknown drivers of the dynamics that could sporadically excite the network in ways that straightforward modeling does not work due to our inability to model non-stationary processes. Towards addressing these challenges, in this paper, we consider the problem of learning the fractional dynamical complex networks under unknown unknowns (i.e., hidden drivers) and partial observability (i.e., only partial data is available). More precisely, we consider a generalized modeling approach of TVCNs consisting of discrete-time fractional dynamical equations and propose an iterative framework to determine the network parameterization and predict the state of the system. We showcase the performance of the proposed framework in the context of task classification using real electroencephalogram data.
[paper] [code]